IFMASS10

339

cable to the heterogeneous of engineering materials structures with various patterns by

multi-field decomposition for describing the material deformation and, ultimately, the

fracture. The potential energy of the system is formulated in terms of micro and macro

stress tensors which account on the deformation gradients, body forces and couples. On

the boundary, the forces and moments are specified together with the geometry and the

volume of the simulation domain.

In this way ab-initio method underlying QM approximations (based on tight-binding

approach) has been coupled with MD and, then, MD model is coupled to macro scale

with continuum FE models. In this approach FE mesh size have been down-scaled to the

interatomic distances range, compare Fig. 6.

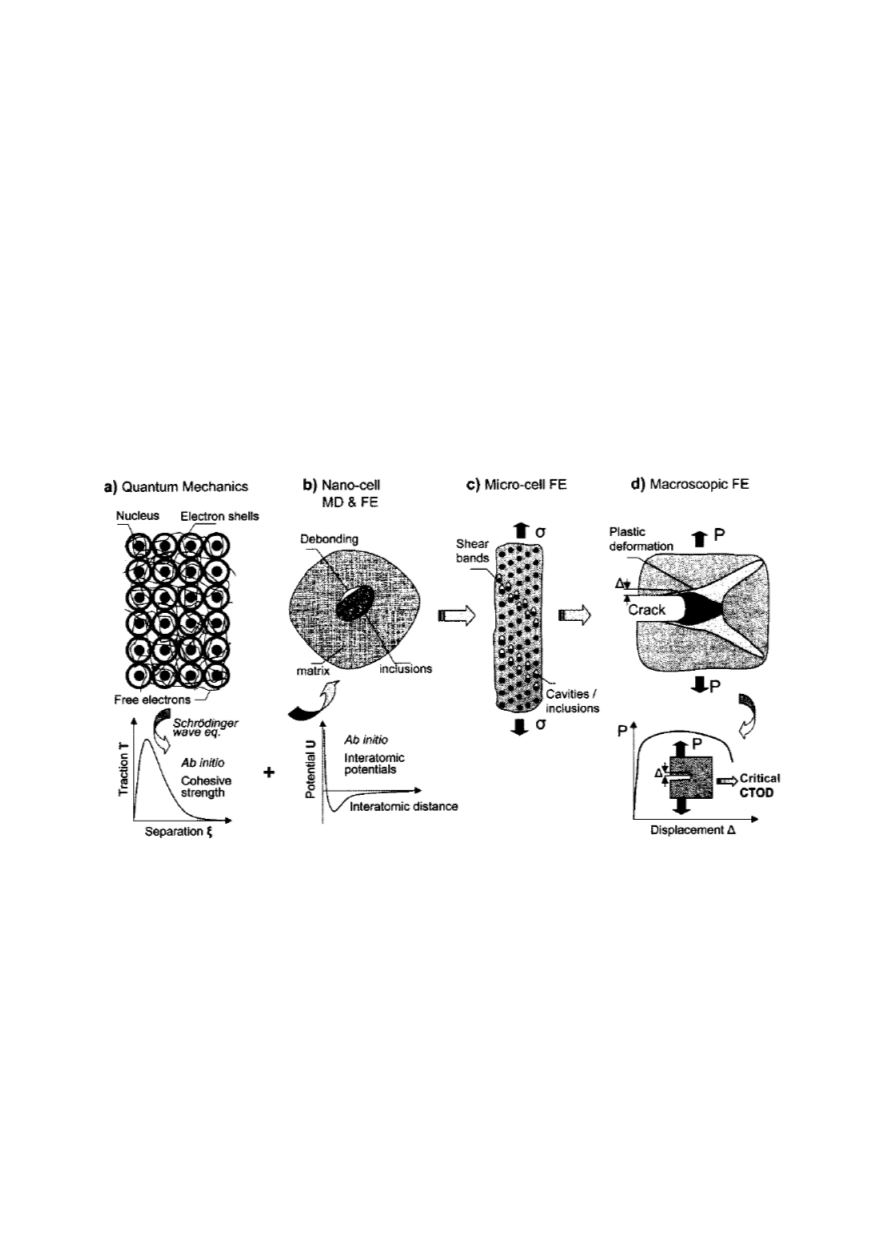
The capacity of this approach is remarkable, as it can be seen from an example of

modelling of deformation and fracture behaviour for material design purpose, applied in

the case of Cybersteel for naval applications (Fig. 18). The steel has been conceived to

contain particles at two different scale lengths. Primary inclusions, order of mean size 1

μm, and nano-secondary particles, order of 0.1 μm, have been considered. The former

enhance the yield point and the tensile strength, the latter improve the ductility,

implicitly the fracture toughness.

Figure 18: Example of hierarchical modelling: quantum mechanics simulation (a); molecular

dynamics and finite elements models (b); macro-cell including nano-cell (c); macroscopic finite

elements model for critical crack opening displacement assessment (d) /1/

For a proper description of localized gradients of deformation, higher-order terms are

included into constitutive equations. The principle of virtual work enables to derive

micro- and macro-scale governing equations. In hierarchical modeling the simulation is

performed independently at every size-scale level by solving the scale-specific constitu-

tive equation. The bridging between levels is achieved by embedding the information

gained by fine-scale simulation into the model of a superior size-scale level.

Hierarchical in combination with concurrent simulation is adequate here since the

failure occurs at several well defined size-scales. Failure initiated by particle-matrix

debonding at quantum scale, void nucleation and growth is typical at mesoscale, shear