IFMASS10

337

of noticeable changes (deformation) or breaking in material, but the structure of nano

material (Fig. 15) requires to describe strength in a way different from that at macro

scale. The problem is in fact that classical strength and strain parameters (yield strength,

ultimate tensile strength, and elongation) are all defined for cross section and length

dimensions, which are in nano materials small and not properly and completely defined

yet.

Safe and reliable service of nano structures is of utmost importance since the conse-

quences of failure can be very difficult, in many cases even catastrophic. Nano structure

can also be defective, and assessment of defect significance is the subject of extended

research and investigation. It is natural to apply gathered experience in the field that

means to apply fracture mechanics approach for structural integrity assessment also at

the nano level scale.

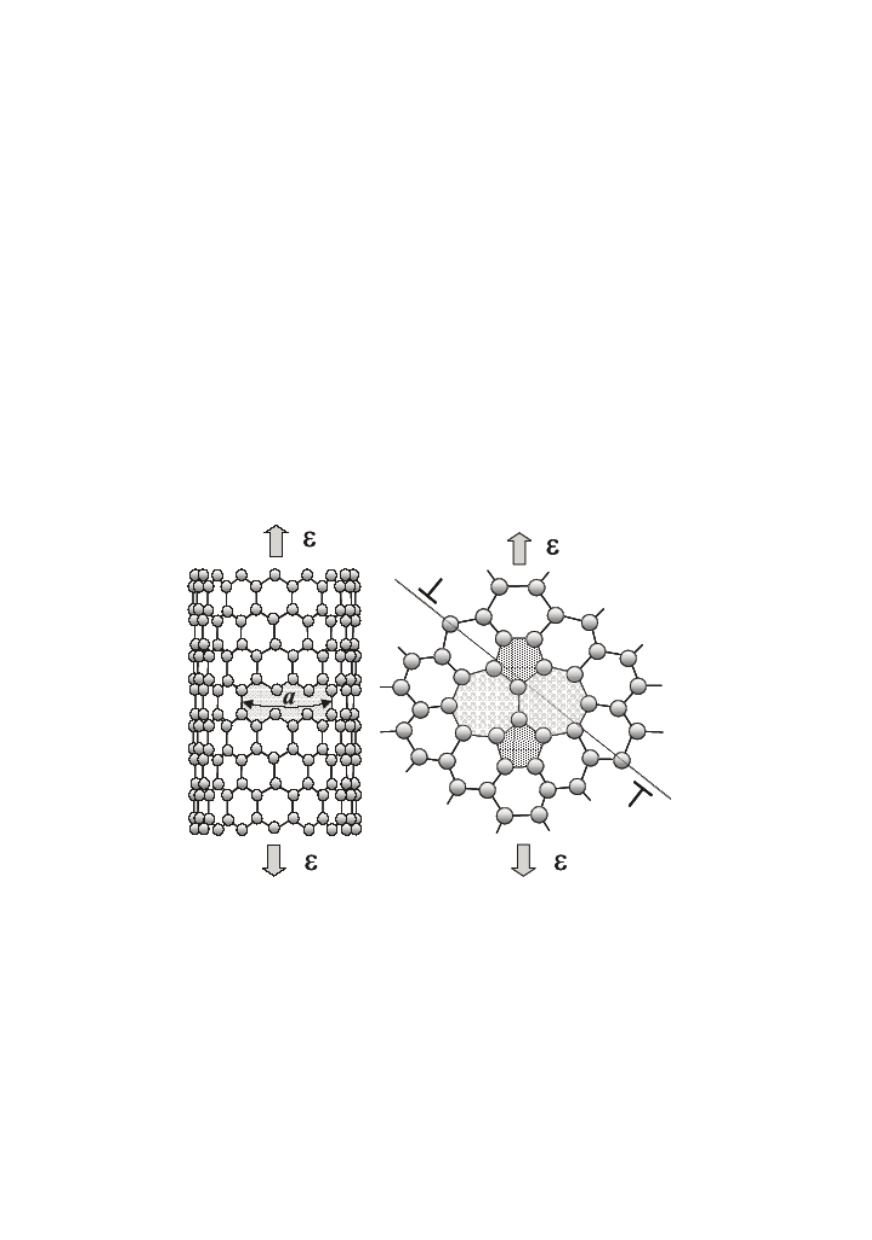
As an example, typical defects which can be introduced in CNT material by axial

straining are presented in Fig. 16 /1/. They are caused

by high axial straining (~15%) and low temperatures (~30K), when longitudinal

bonds can be broken producing conventional crack-like defect of length

, and

by thermally activated accommodation to applied strain at higher temperatures

producing carbon atoms re-arrangement in a distorted configuration of two pentagons

and heptagons with the generation of an edge dislocation dipole.

Figure 16: Defects generated in CNTs by axial straining: longitudinal bonds break producing a

crack of length

(left) and thermally activated accommodation producing an edge dislocation

dipole (right) /1/

The change of basic mechanical properties and material response to loading in this

situation is inevitable.

Crack size and tip region are very small when considered in a sample of macro- up to

the micro- scale (Fig. 13). This allows to treat material as continuous solid and apply the

analysis of stresses, strains and cracks as defined in mathematical and numerical models,

in spite of series of accepted simplifications. It is also possible to assume that crack tip

exists as singular point in continuum solid, producing shortly described consequences on