
341
It is to notice assumptions involved at different scale, generally in tending to be suffici-
ently conservative to assure requested safety and reliability.
5.2. Reconsideration of Griffith’s model
Since the size of the nano-structures becomes comparable to the size of the cohesive
zone near a crack tip new approaches for the prediction of crack propagation are offered.
In addition to the model presented in Fig. 14, next model is proposed by N. Pugno et al.
/24/ as a modification of Griffith theory. If the load exceeds a critical value at which a
crack of given length is stable, the energy-release rate per unit area of crack advance,
G
,
becomes larger than the intrinsic crack resistance,
G
c
and as a consequence the crack
propagates. In a perfect homogeneous solid in vacuum the crack resistance energy per
unit surface is identified with the cleavage surface energy
γ
. Crack resistance is defined
as
G
c
= 2
γ
c
. Within LEFM it is assumed that
γ
c
=
γ
. Quantized fracture mechanics (QFM),
that modifies continuum-based fracture mechanics substituting the differential in Griffith
criterion with finite difference has been formulated in /25/. This simple assumption has
remarkable implications: fracture of tiny systems with a given geometry and loading
conditions occurs at quantized stresses that are well predicted by QFM. The QFM theory
introduces a quantization of the Griffith criterion to account for discrete crack propaga-
tion and discontinuous nature of matter at the atomic scale, and thus in the continuum
hypothesis differentials are substituted with finite differences.
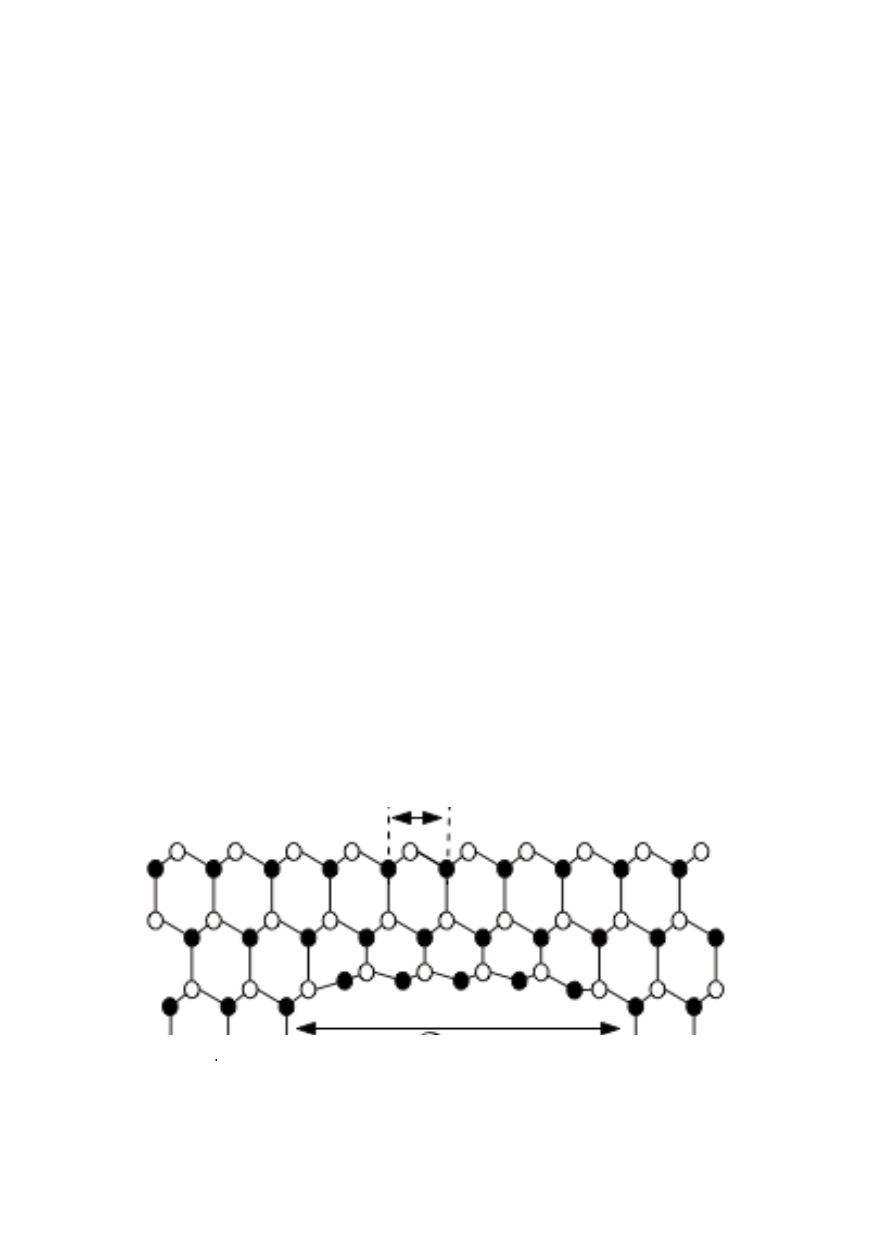
Simulations with nanocracks of length 2
c
0
< 2a < 50
c
0
, where
c
0
= 0.2644 nm for
silicon carbide matrix shown in Fig. 19, were performed using the Tersoff potential for
calculation of inter-atomic forces /25/. Obtained results have shown a departure of 25%
from the Griffith theory.
Modern atomistic methods and continuum methods for nanoscale modelling and
simulation provide many insights about behaviour of the cracks on the nano-scale /16/.
Continuum methods often start with extending the range of applicability of proven
engineering methodologies to nanoscale phenomena. The recently developed Virtual-
Internal-Bond (VIB) method is aimed to investigating fracture of such nano-materials. It is
demonstrated that, at a critical length scale typically on the order of nanometer scale, the
fracture mechanism changes from the classical Griffith fracture to one of homogeneous
failure near the theoretical strength of solids.
2
a
Figure 19: Geometry of the Griffith problem in the atomic-scale Full (open) dots represent carbon
(silicon) atoms; the bond network is represented by sticks


















