
27
mostly applied in USA. It is interesting that these two parameters are related in definite
functional way, so that both could be applied, and proper application must lead to the
same results. This, however, does not mean that the both procedures are the same.
3.2.
J
- integral
The stress-strain relationships in the theory of plasticity are much more complex than
that for elastic theory. For example, when a material deforms elastically, it is possible
based on current strains to determine current stresses and vice-versa. In case of plasticity
this is not possible, because the material response to plastic deformations is history
dependent. For that, the same combination of deformations can include different stress
states. Based on this, it is not possible to achieve analytical solution for the crack tip
stress field, similar to the solution for linear elastic materials. It is necessary to use the
approximate solutions, like for non-linear elastic material or for deformation theory
(Chapter 2.2.). Given solution certainly does not have general character, especially for the
cases of 3-dimensionl geometry, but there are many situations in which non-linear elastic
material model supply solid approximation for real material behaviour.
Rice utilised this approximation to derive the
J
path independent
integral (Fig. 9), a
parameter that describes the conditions near the crack tip in a proper way.
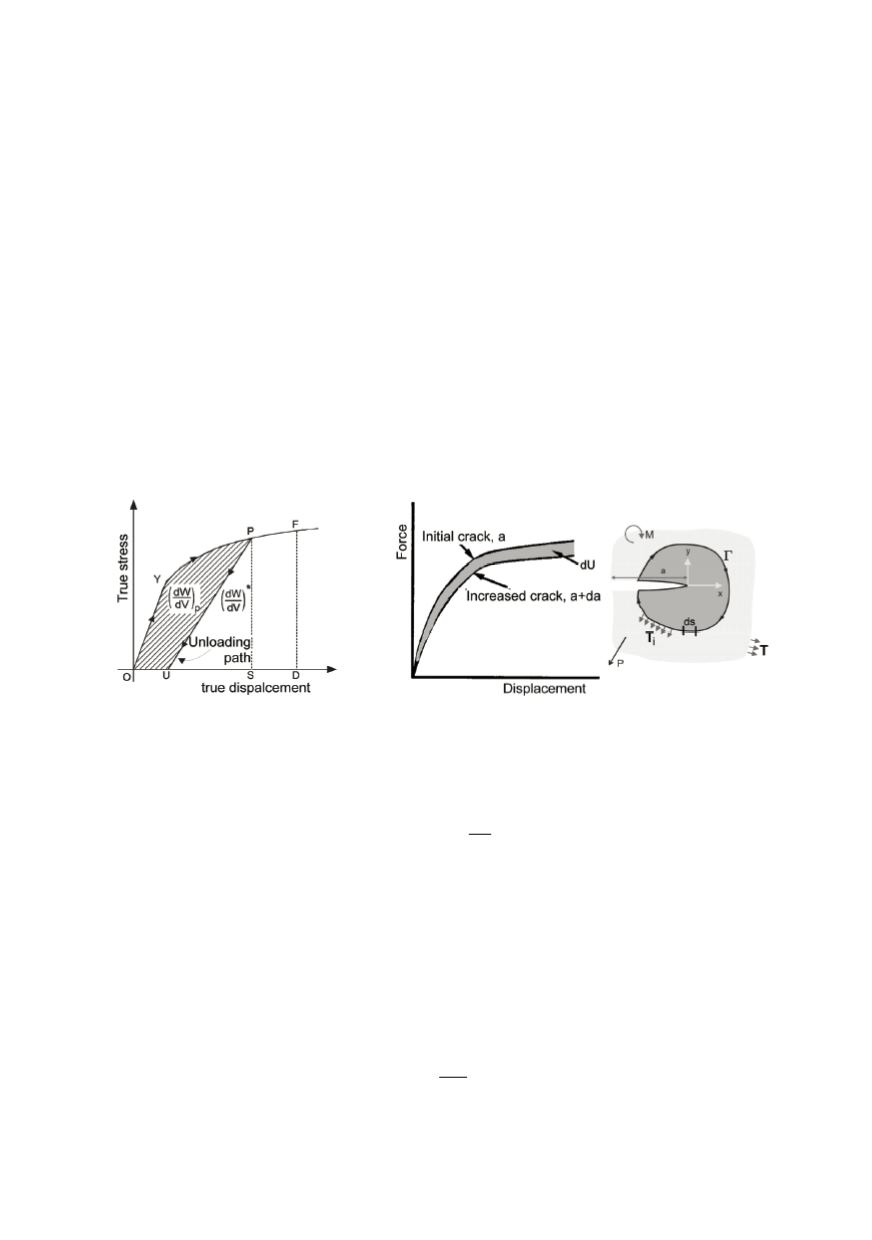
Figure 8. Energy for crack growth
Figure 9. Elements for
J
- integral evaluation
In fact, class of path independent integrals was earlier known, but not applied to the
solution of fracture mechanics problems. The
J
- integral value is obtained by integrating
the following expression along an arbitrary closed path (Fig. 9) around the tip of a crack
u
J Wdy T ds
x
Γ
∂
⎛
⎞
=
− ⎜
⎟ ∂
⎝
⎠
∫
(13)
where
Γ
represents the path of integration (it is important to observe that within
Γ
there is
no singularity), and
W
is the strain energy density. Furthermore,
T
is the traction vector,
u
is the displacement vector and
ds
increment along the path contour. For non-linear elastic
materials Rice showed that the value of
J
is independent of the integration path as long as
the contour encloses the crack tip.
J
represents energy release rate of nominal potential energy depending on crack
growth (for thickness unit of crack contour) for non-linear elastic body.
J
can also be
imagined as the energy that flows into crack tip.
U J
a
Δ
∂⎛ ⎞
= − ⎜ ⎟ ∂⎝ ⎠
(14)


















