IFMASS10

is possible, even though the effective

value does not have any connection with the

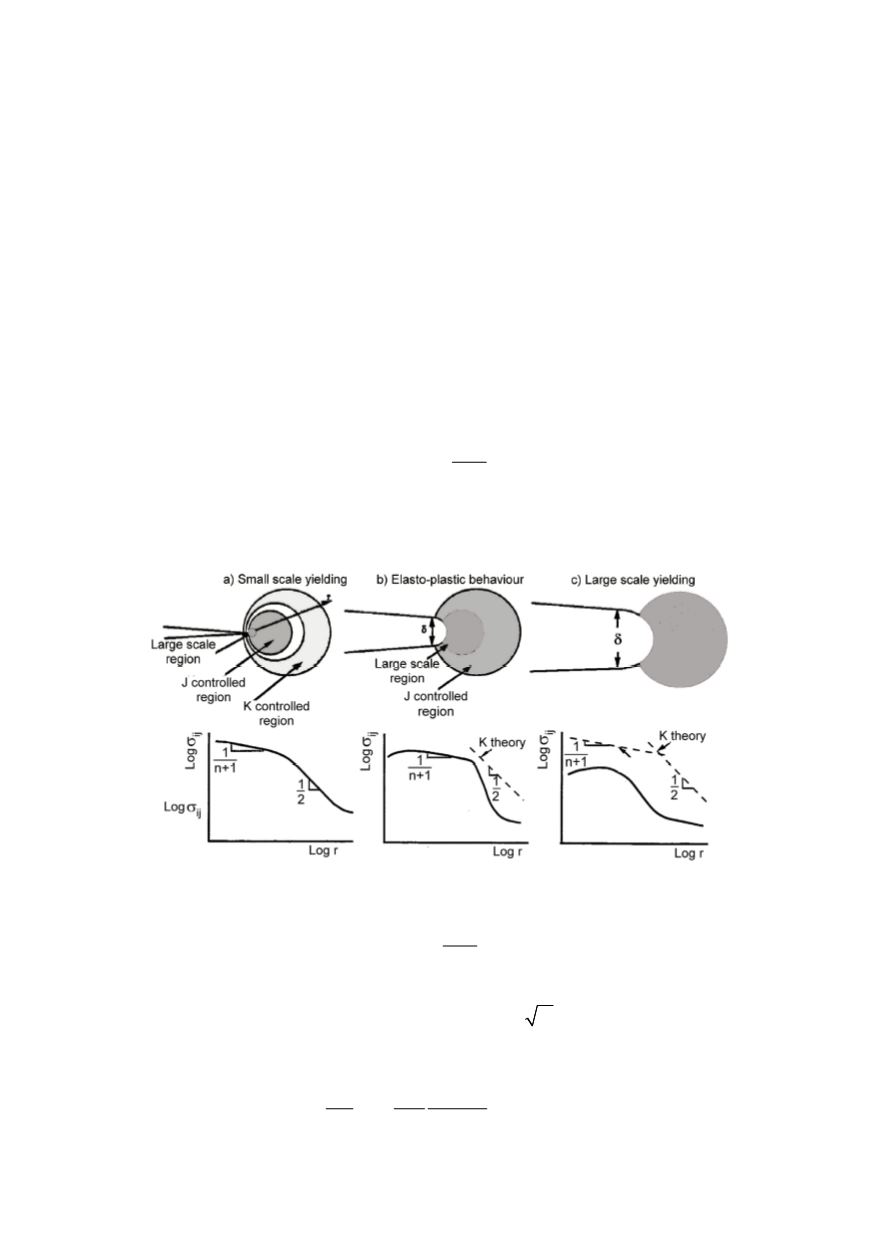
stress distribution around crack tip shown by broken line in Fig. 10 b).

In addition, region on the tip, not controlled by the solution is becoming much larger,

HRR solution is no more valid in this area due to the crack blunting. It is favourable that

the stresses in the large strain region are lower than predicted by the HRR singularity.

Under large scale yielding conditions, Fig. 10c, the calculations both with

and

are

no more valid. If the material is sufficiently ductile to experience this state before fractu-

re, than the stresses at the tip are significantly favourable, not only because of lower

values (than predicted by both

and

theory) but also because of a loss in triaxiality.

The sizes of the

and

controlled regions depend on the size and geometry of the

structure with the crack. Based on larger dimensions these regions in case of real

structures exist considerable longer, and because of this for the evaluation of material

characteristics the specimen must satisfy corresponding conditions for its validity to the

real structures be guaranteed. For example, for

evaluation different standards require

that the specimen dimensions fulfil the following requirement:

2.5

B b

⎛

⎞

≥ ⎜

⎟

⎝

⎠

(20)

where

is the specimen thickness and

the size of the uncracked ligament. Comparison

with the plastic zone correction shows that these should be no more than 1/50 of

specimen characteristic dimensions.

Figure 10: Scheme of the effect of plastic deformation on the crack tip stress field

For

evaluation requirements concerning the specimen size are different:

25 ,

B b

≥

(21)

where

is the flow stress, defined as the average between the yield and tensile strengths.

For mild steels with

= 350 MPa,

= 250 MPa

and

= 210 GPa according

this requirement, specimen size for

evaluation should be

B, b >

1.28 m

For

evaluation, however sufficient sizes of the specimen are:

(1 )

0.02 m

−