IFMASS10

127

neglects finite geometry changes at the crack tip based on its blunting. The validity of the

solution is loosed already before the end of plastic zone. When the contribution of the

higher order terms in the series become significant, this isolated parameter is no more

sufficient for the more accurate evaluation of the stresses in the section, but also for the

assessment of the important effects based on constraint, like geometry parameters of the

cracked body (this means not only constraint due to the wall thickness). This led to the

so-called two parameters fracture mechanics, of which the most known are

for the

correction of

and

for the correction of J-integral.

The dependence on the geometry in LEFM conditions emphasize the importance of

another aspect, not sufficiently respected up to now. Theoretical analysis of notch or

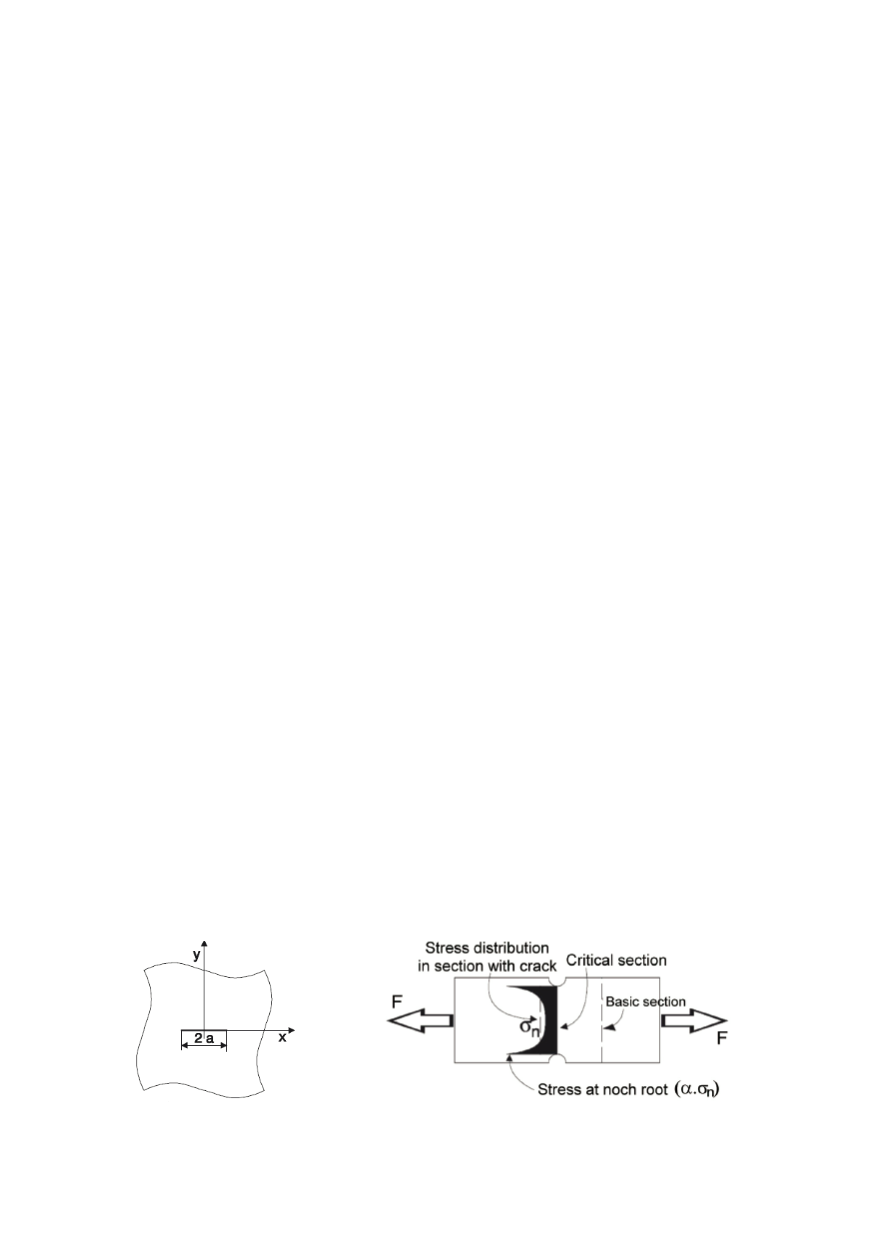
crack starts from the assumption of endless contour in the space (Fig. 1). Nominal stress

is evaluated independently of the crack effect.

In the reality the solid is always of limited size, and for the purpose of evaluation

under the real conditions different corrections are introduced, like that for plate width and

back wall. Unfortunately, this kind of correction is developed only for LEFM and is

inaccurate under the yielding conditions. The corresponding solutions are in general not

analytical, but based on finite element calculations or experiments. As already shown, at

very short distance from the crack tip the solutions based on

and

is no more valid and

significant differences appear here, depending on local geometry. In addition, signifi-

cance of the stress in the cross-section weakened by the crack is obvious having in mind

that for the evaluation of the collapse or pure plastic failure must be considered, although

the definition of the corresponding stress is often not simple and accurate.

Elastic-plastic fracture analyses such as given in the EFRI or R-6 methods assume net-

section yielding in the structure. According to the definition,

is the ratio of the applied

load to the load which produces plastic yielding of the cracked structure, so that the

weakening of the section by the crack must be considered.

However, in the calculation of the Fracture-Analysis-Diagram (FAD) it is usual to

take the ratio of equivalent applied stress to the material's yield or proof strength, and not

the section forces, so the smallest section is compelling. The solutions for

values are

standardized in the fracture mechanics, considering stress in the section without crack.

Similar problem is well known by the treatment of material fatigue (Fig. 2).

Under the condition of local plasticity the evaluation of maximal stresses and strains

due to the stress concentration caused by notch or hole in the plate is based on the stress,

reached in the section reduced by the hole or notch, calculated for a particular loading

with stress distribution across the section obtained for a uniform geometry. This is especi-

ally important when, for example, the mean stress effect has to be considered. Because of

this following question is reasonable: why the stress in critical section is not calculated

based on elastic-plastic fracture mechanics?

Figure 1: Crack theoretical model

Figure 2: Presentation of stress concentration effect