
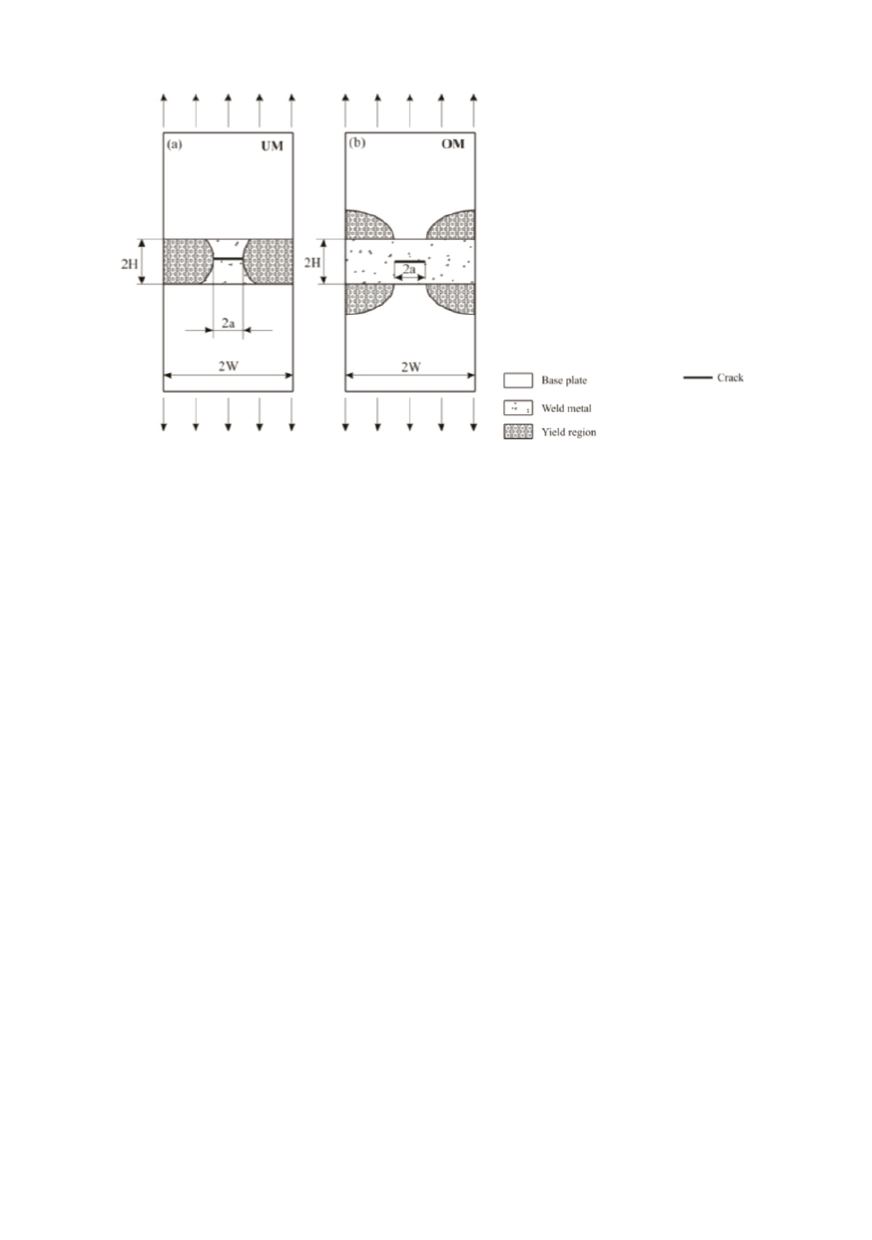
120
Figure 17: The mechanical consequences of strength mismatch
the latter given as
σ
Y
=
R
eL
for materials with Lüders plateau, and
σ
Y
=
R
p0.2
without it.
6.6. Stress intensity factor
K
The SINTAP procedure provides an own compilation of stress intensity factor,
K
, and
limit load solutions. Stress intensity factors can be determined for single load, like force,
bending moment, internal pressure, as well as for stress profiles. The latter alternative
allows consider geometrically complex components by using substitute structures, i.e. the
stress profile is determined for the real structure without crack, whereas the determination
of the
K
-factor is based on a simpler geometry like a plate or a cylinder.
6.7. Correction function
f
(
L
r
)
Under conditions of small scale yielding (roughly up to 0.6 times the limit load) a
fracture mechanics analysis can be based on the linear-elastic
K
factor. For contained and
net section yielding where the plastic zone is no more limited to a small region ahead of
the crack tip, the application of the
K
concept would lead to a significant underestimation
of the real crack tip loading in terms of the
J
-integral or CTOD. Irrespective of this gene-
ral statement the application of a formal
K
concept becomes possible when the linear-
elastic
K
factor is corrected with respect of the yield effect. This is the essential of the
correction function
f
(
L
r
). With respect of
f
(
L
r
) the SINTAP procedure is structured in a
hierarchic manner consisting of various analysis levels constituted by the quality and
completeness of the required input information. Higher levels are more advanced than
lower levels: they need more complex input data, but the user is "rewarded" by less con-
servative results. An unacceptable result provides a motivation for repeating the analysis
at the next higher level rather than claiming the component to be unsafe.
Default level
The corresponding equations for
f
(
L
r
) for ferritic steels without Lüders plateau are:


















