IFMASS10

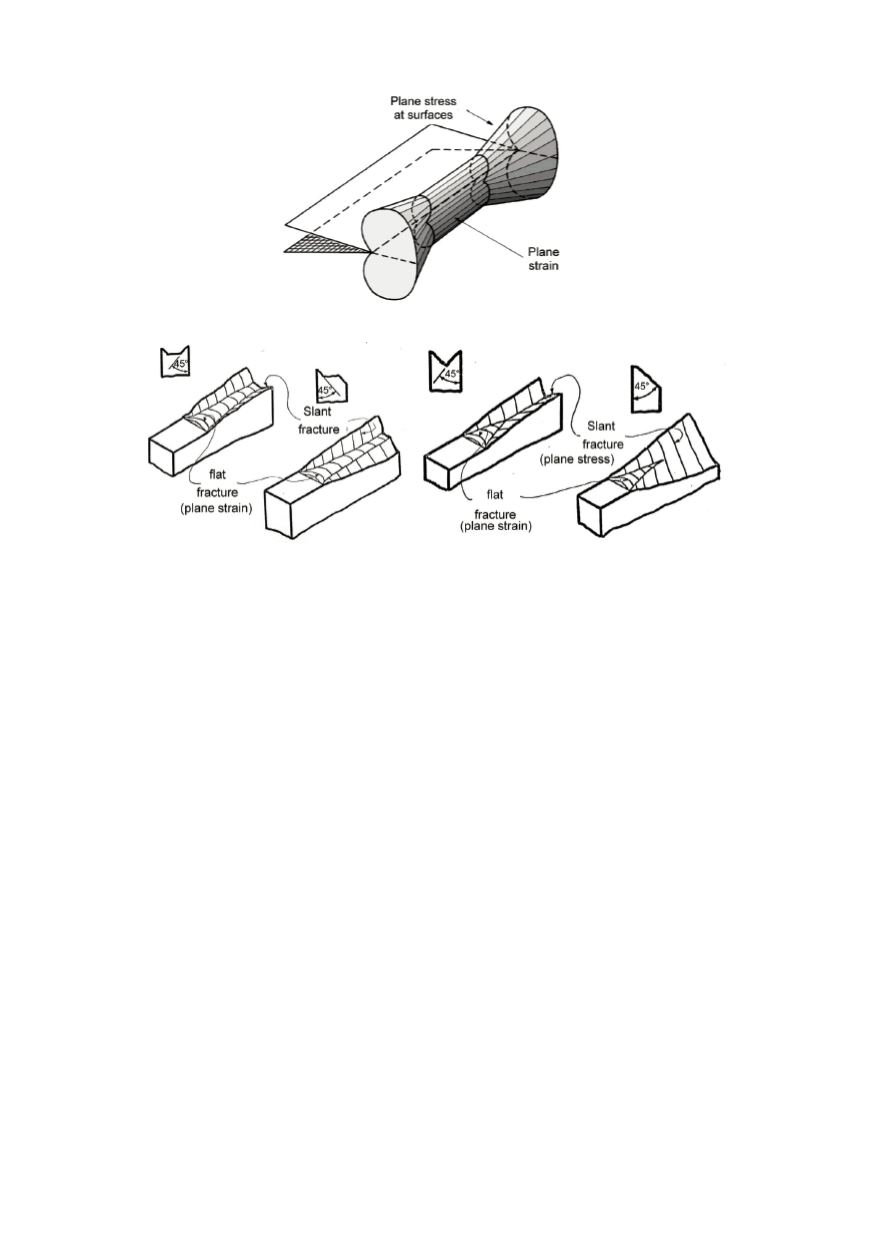
Figure 20: Through thickness plastic zone in a plate

Figure 21: Typical forms of the fracture surface for plate or thin wall structure

The crack surface is observed to rotate in this region so as to make an angle of

approximately 45° with load direction. These inclined portions of the crack surface near

the plate surfaces are known as "shear lips". The proportions of each type of crack surface

depend on material properties (yield strength, strain hardening exponent), specimen

geometry (crack length, plate thickness) and loading. The proportion of the fracture

surface associated with slant fracture or shear lips increases with decreasing plate

thickness and in very thin plates in which the shear lips merge into each other the fracture

surface completely rotate to 45°. The initial straight fracture line decreases with increase

in load level, showing the dependence of the behaviour on load level.

The postulates that "plane strain condition" are in all cases on the safe side cannot be

fully accepted, as it refers only to "out-of-plane" constraint which are normal to the crack

growth direction, and does not allow for explaining the effects of varying "in-plane"

constraint in the direction of crack growth. Anyway, specimens for fracture toughness

measurement the corresponding requirements in both directions must be fulfilled.

Although, the constraint problem is connected to the stress state in space and to the

effect of hydrostatic stresses, the first attempts to take this phenomenon into account were

based on the solutions for

and

. As known the solution based on

is realised by

neglecting higher terms in the solution, and the solution for

with the assumption for

non-linear elastic material. Based on this, the parameters

-stress and

-factor has been

involved to consider the neglected parts of the solution and so ignored effects of

geometry and load level. Application of these parameters have demonstrated that scatter

of experimental data can be significantly reduced by correcting for constraint effects.

The two-parameter formulation based on the

-stress approach is defined through the

expansion of the linear elastic stress field about the crack tip using the form