
36
of the mean volume (hydrostatic) stress
σ
m
relative to the resulting von Mises effective
stress,
σ
e
, i.e.
h =
σ
m
/
σ
e
. According to plastic theory laws, especially in case of metals, the
mean „hydrostatic“ stress of the system will never cause yield, no matter how large the
stress. Therefore, the size of plastic increments depends only on components of the so-
called deviatoric stress, and in the case
h =
1 plastic deformation will not occur.
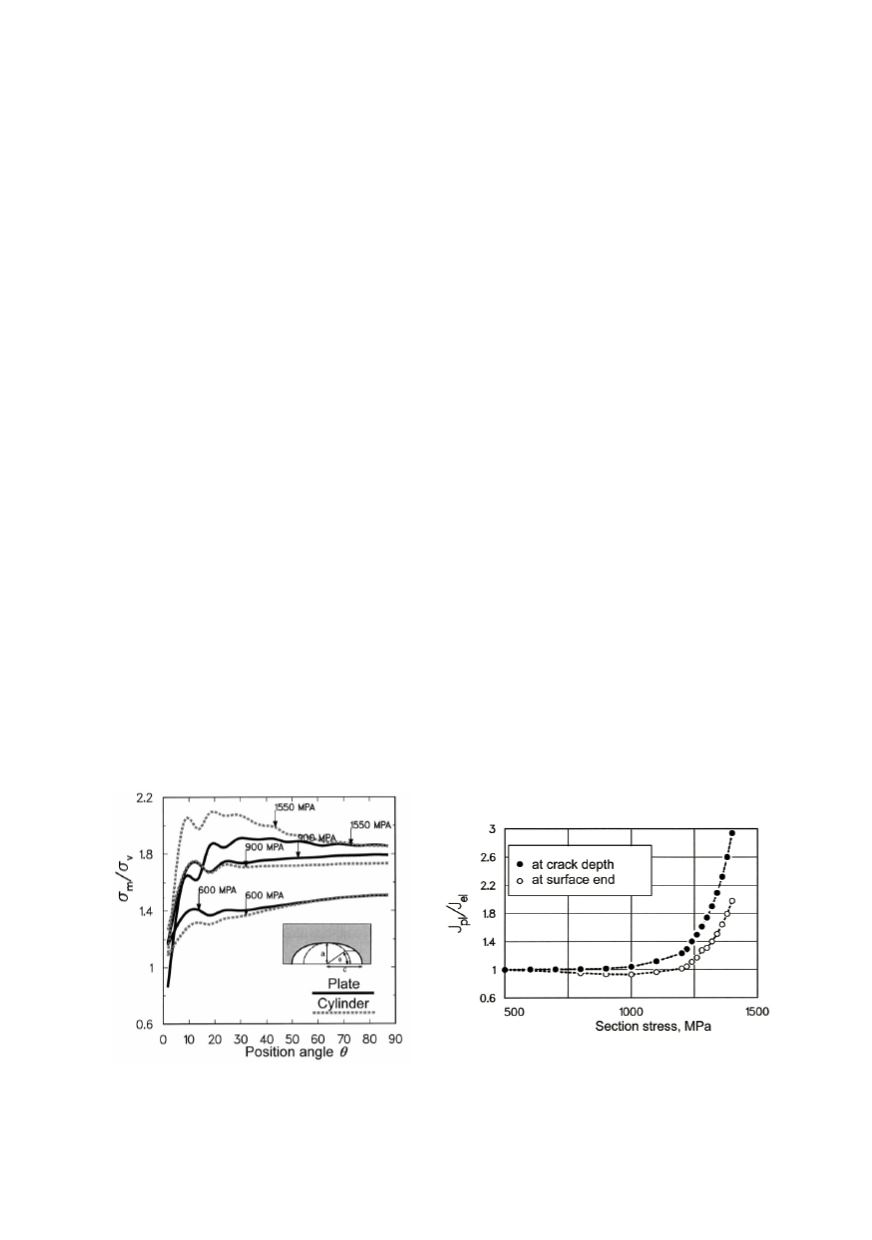
Complexity of the conditions for volume cracks shows the results of FEM-calculation
for surface crack in Fig. 18. Near the surface the yielding is free and
h
takes minimal
values. However, the value of the constraint parameter
h
increase inside the crack, what is
not difficult to imagine, and in case of cylinder under pressure the maximal values is even
between surface and depth (ligament) of the crack. The consequences of this are shown in
Fig. 19. In spite of load increase the values of
J
- integral at the surface are on account of
plasticity in decrease and only after crossing into full plasticity increase arise that,
however, fall back compared to the crack depth position. Obviously, the application of
elastic solution (
K
) is not sufficient to evaluate relationship along crack contour.
High degree of constraint leads to the faster fracture. Because the energy introduced in
system (the value is measured by
J
- integral) is dissipated based on plastic deformation
in smaller extent, and therefore stay available for fracture initiation. It is obvious that the
constraint is significant parameter for fracture mechanics to establish the safe fracture
criteria. But, important problem exist, because of the constraint conditions for specimens,
which are small, compared to the real structure, so that the data transfer could be unsafe.
The constraint effect is observed from early beginning of the fracture mechanics
development. Limitation to the 2-dimesional through crack showed the consequences
already by the selection of specimens. However, former only two extreme cases, plane
stress and plane strain has been shown to be insufficient.
Figure 20 shows that, due to different conditions on the external surfaces and inside of
the specimen the size of the plastic zones is different, and material resistance at specimen
surfaces is higher than inside it. In Fig. 21 various forms of fracture surfaces for 2-
dimensional specimens are shown. An initially straight front bends at ends with the
growth before the instable fracture onset. Interior to the plate, there prevails a high
constraint effect leading to crack growth profile similar to the beginning. At specimen
edges there is no constraint and the energy is more dissipated in distortion.
Figure 18. Degree of constraint along crack
profile (comparison of plate and cylinder)
Figure 19.
J
- integral development for situations
in Fig. 18


















