
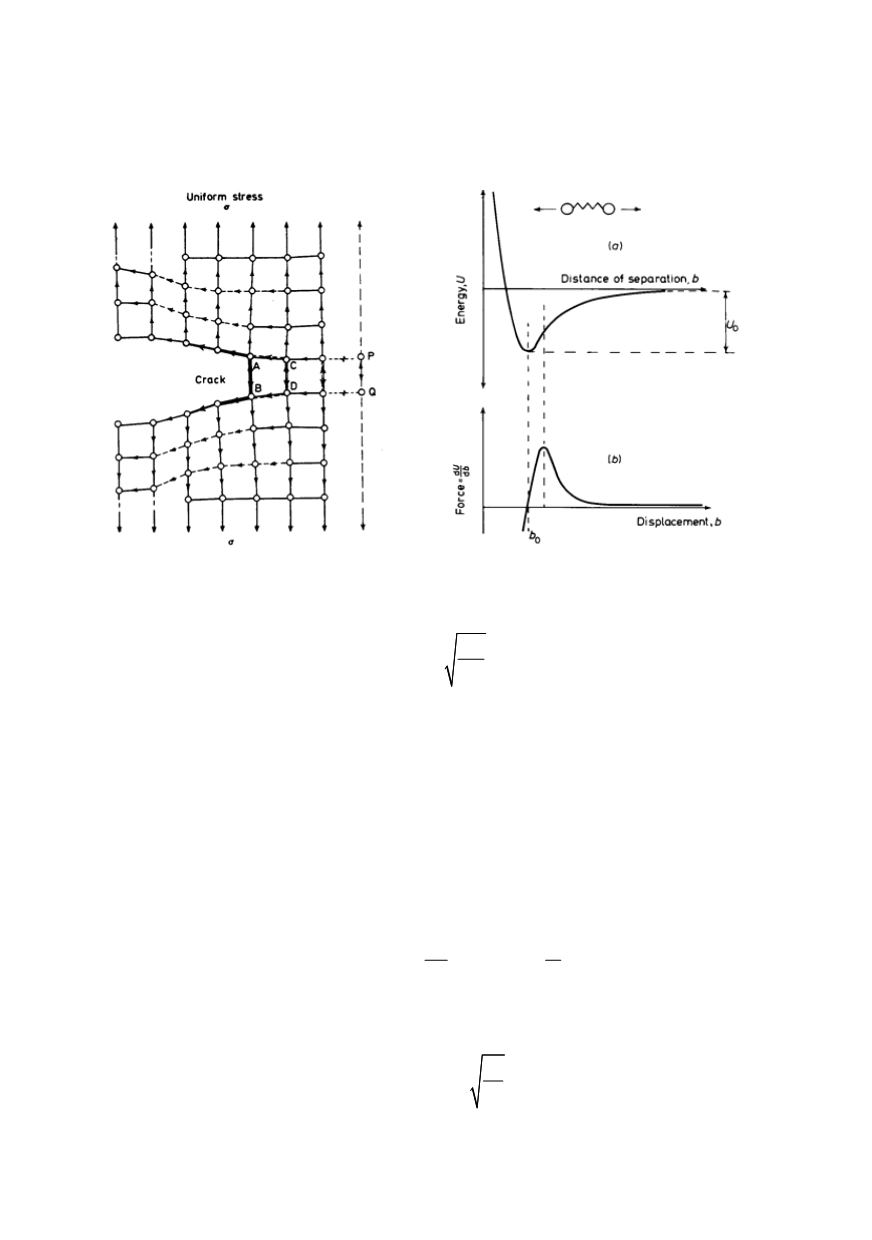
327
distance between atoms
b
, and the total energy, necessary to separate the two atoms to
infinity, is given by
U
o
. The derivative of this curve is force – displacement curve, with
initial slope equal to elasticity modulus
E
and total area under it is equal to twice the
surface tension, 2
γ
, considering both sides of extended crack.
Figure 6. Development of a crack in an
atomic model
Figure 7. Bonding energy vs. distance of separation
(up) and force vs. displacement (down)
Next approximation enables to derive the relationship /10/
max
o
E
b
γ
σ
=
(4)
where
σ
max
is ideal strength of material, and approximate fracture stress
.
Fracture stress value of the order of
E
/10 may be estimated from Eq. (4), using the
value of
γ
of the order 0.01
⋅
Eb
o
, applicable to many metals. The strengths of crystals and
glasses in practice tend to be lower than this value by two orders of magnitude. Griffith
/7/ first suggested that a macroscopically homogeneous sample might contain small
defects, a cause of discrepancy between predicted and actual values because ideal
fracture stress can be attained only locally in the sample.
To understand the fracture stress let us suppose an infinite body with a defect of
elliptical shape (Fig. 4), with major axis 2
a
and minor axis 2
b
, lying normal to the
applied stress,
σ
. The concentrated value of stress at the ellipse ends would be /7/
1 2
2 1
1 2
/
yy
max
a
a
b
σ
σ
σ
σ
ρ
⎡
⎤
⎛ ⎞
⎛
⎞ ⎢
⎥
= = + = + ⎜ ⎟
⎜
⎟ ⎢
⎥
⎝
⎠
⎝ ⎠
⎣
⎦
(5)
where
ρ
=
b
2
/
a
is the radius of the ellipse tip. For crack-like defect, a value for
ρ
is taken
as the lattice spacing
b
o
. Then, since 2
√
(a/b
o
)
>> 1 one would obtain:
2
yy
max
o
a
b
σ
σ
σ
= ≅
(6)


















