IFMASS10

314

the results given for a discrete model of cohesive crack reduce to the known equations

valid when discretization is removed. This is done by letting the fracture quantum

approach zero and thus considering the range of

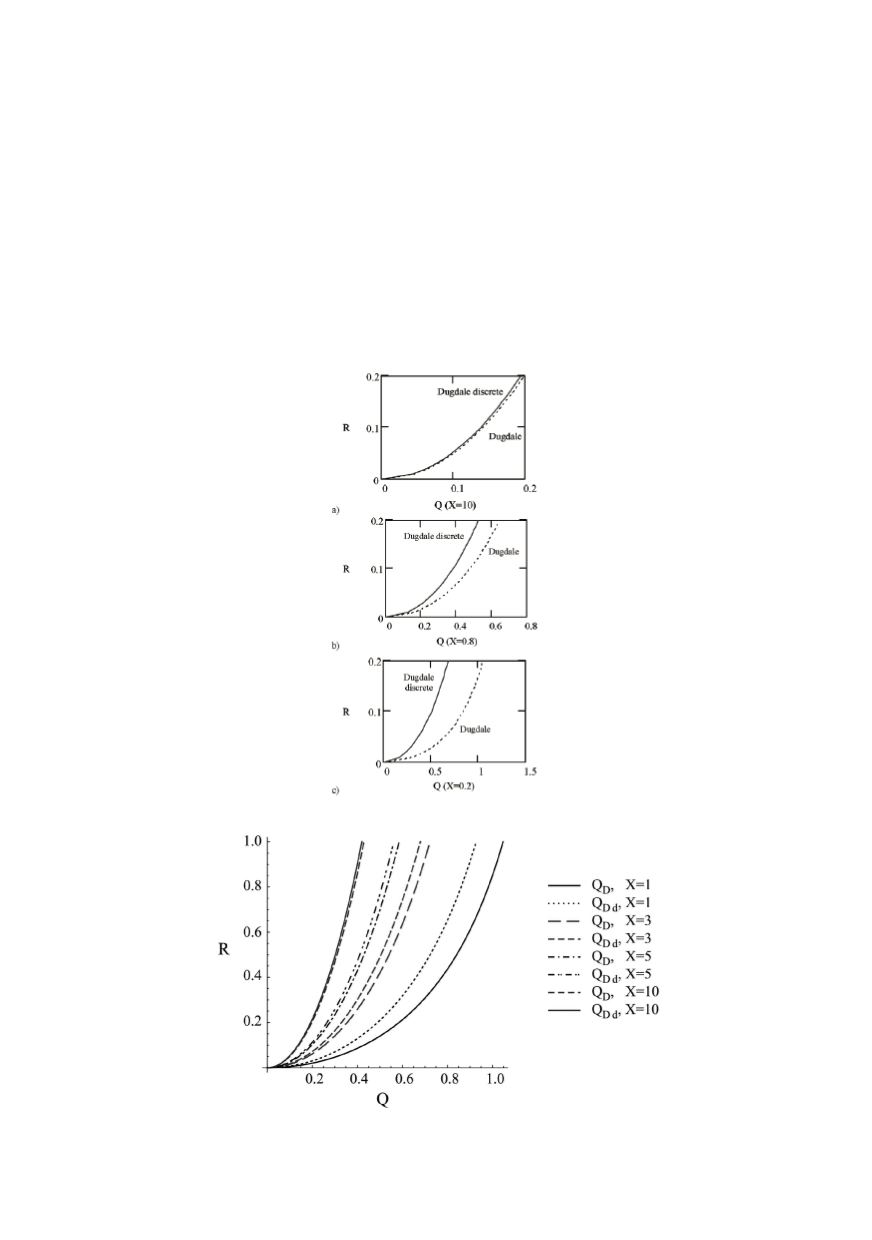
- > infinity. Figure 2 illustrates the

differences and similarities between the solutions obtained from the discrete cohesive

crack model and the classic Dugdale model. Examination of the graphs shown in Fig. 2

reveals that for a given external load

, the nondimensional length of the cohesive zone

(which remains in equilibrium with the applied load) is greater for the discrete model.

Thus the measure of the material resistance to crack initiation is enhanced when the

discrete nature of fracture is taken into account. Naturally, the differences are more

pronounced for the nano scale levels when the initial crack length is comparable to the

magnitude of the fracture quantum; examine graphs (a), (b) and (c) in Fig. 2. The same

conclusions would be drawn from examination of Fig. 3.

Figure 2: The comparison of discrete cohesive crack model and the classic Dugdale model

Figure 3: The analysis of graphs (a), (b) and (c) from Fig. 2