IFMASS10

317 / 352

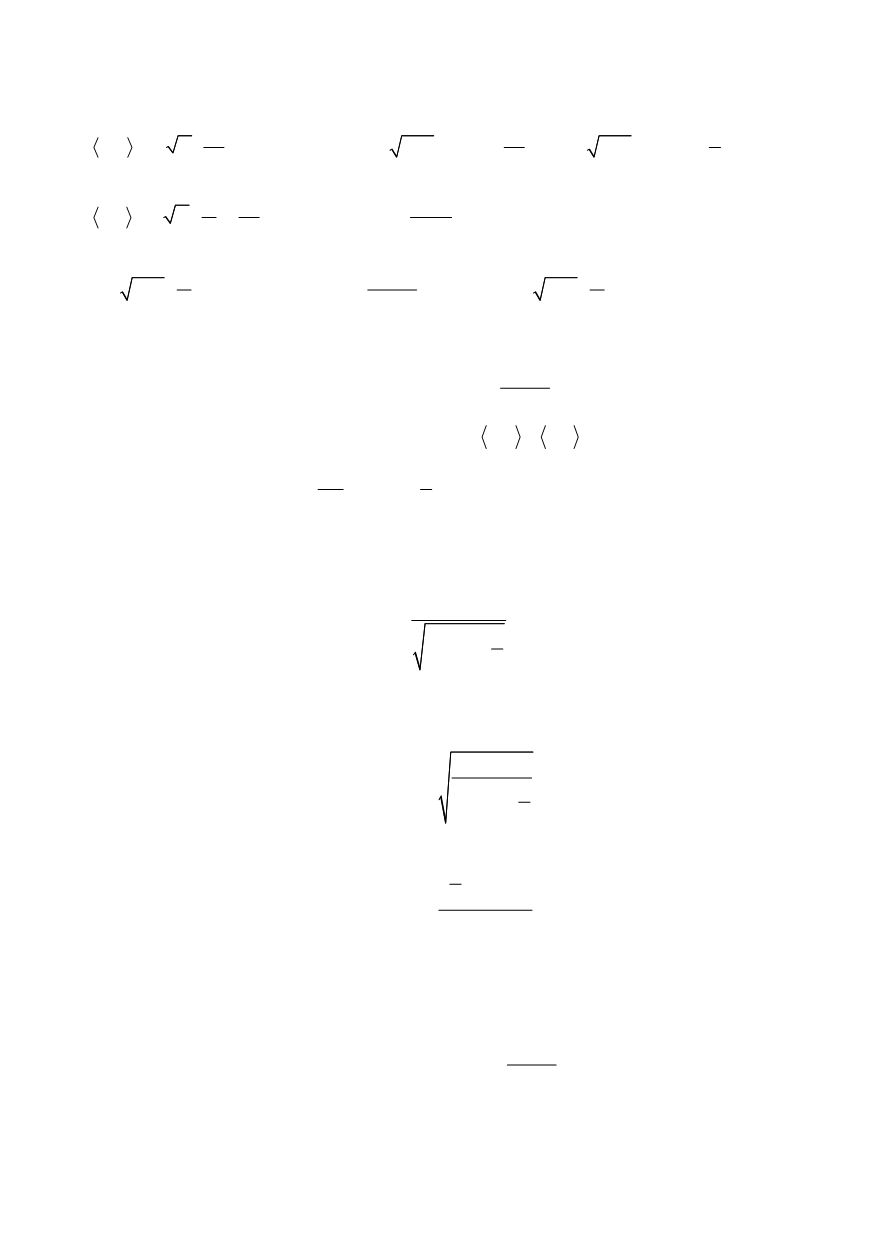
313
The results are
j i 0 1/2 1/2 1/2
0
0 0
0
1 1
( )
2 2
c a
c
a
K c R dc a c R a X R
a σ σ π σ π σ π
+ ⎡ ⎤ ⎛ ⎞ ⎛ ⎞
= + = + + = + +
⎢ ⎥ ⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠
⎣ ⎦
∫
i
i
( )
0
1/2
2
1
0
1/2
2
1
1 1/2
0 0
2 1 ( ) cos
2 2
cos ( , )
c a
S
c
X
X
c
K S c R dc
a c R
X
S a X R dX S a I X R
X R
π
π
π π
π π
+
−
+
−
⎧ ⎫
⎡ ⎤ ⎪ ⎪ ⎛ ⎞ ⎛ ⎞
= + =
⎨ ⎬ ⎜ ⎟ ⎜ ⎟ ⎢ ⎥ +
⎝ ⎠ ⎝ ⎠ ⎣ ⎦ ⎪ ⎪
⎩ ⎭
⎧ ⎫
⎡ ⎤ ⎪ ⎪ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞
= + =
⎨ ⎬ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎢ ⎥ +
⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎣ ⎦
⎪ ⎪
⎩ ⎭
∫
∫
(13)
The auxiliary integral I(X, R) is defined as follows
( )
2
1
1
( , ) cos
X
X
X
I X R X R dX
X R
+
− ⎡ ⎤ ⎛ ⎞
= + ⎜ ⎟ ⎢ ⎥ + ⎝
⎠ ⎣ ⎦
∫ (14)
Substituting (13) into the equilibrium equation S K Kσ = yields
1/2
1/2 1 ( , )
2 2
X R I X R
S
σπ⎡ ⎤
+ + =
⎢ ⎥
⎣ ⎦
(15)
One can readily solve this equation for the loading parameter Q as a function of X and
R. To distinguish this solution from the classic Dugdale solution (10) the subscript D is
used for “Dugdale” and the superscript “d” for “discrete”. From (15) it follows
1/2
( , )
1
2
d
D
I X R
Q
X R
=
+ +
(16)
An interesting simplification of Eq. (16) is obtained for the limiting case of small
ratios R/X. For this case the integral (14) reduces to 2 R, and thus the Eq. (16) can be re-
written as follows
2
1
2
d
D R X
R
Q
X R
⎡ ⎤ =
⎣ ⎦
+ +
(17)
The inverse relationship can be readily provided
2
2
1
2
2
d
D X R
X Q
R
Q
⎛ ⎞ + ⎜
⎟
⎝ ⎠
⎡ ⎤ =
⎣ ⎦ −
(18)
The other interesting result is obtained for the asymptotic case of X >> 1, i.e., for the
situation when the fracture quantum a 0 vanishes. When this case is tested numerically it
transpires that the Eq. (16) reduces to a form identical with the Dugdale result (10). For X
>> 1 one gets
1
1
cos d
D D
X
X
Q Q
X R
− ⎛ ⎞
⎡ ⎤ → = ⎜ ⎟ ⎣ ⎦ + ⎝⎠
(19)
The inverse relation would agree with Eq. (10). The subscript D has been added to the
symbol Q to identify it with the Dugdale result. It is therefore justified to conclude that