
320
In a classic LEFM crack model there is no cohesive zone, and the crack itself provides
a mechanism for relaxing the high stresses in the vicinity of a stress concentration.
Therefore, this representation may be thought of as a limiting case of a more general and
refined mathematical formulation involving cohesive zone associated with a crack. For
such a representation the equilibrium between the driving force
K
σ
2
and material resis-
tance
K
S
2
defines a unique relation between the length of the cohesion zone, say
R
, and
the applied load, say
Q
. The equilibrium between
R
(=
R/
a
0
) and
Q
is maintained during
the loading process up to the point of incipient fracture.
Cohesive zone generated prior to fracture has two important aspects. It measures the
material resistance to fracture: the longer is the cohesive zone, the greater is the resis-
tance. It also provides a mechanism for relaxing stresses prior to fracture in the immediate
vicinity of a stress concentrator.
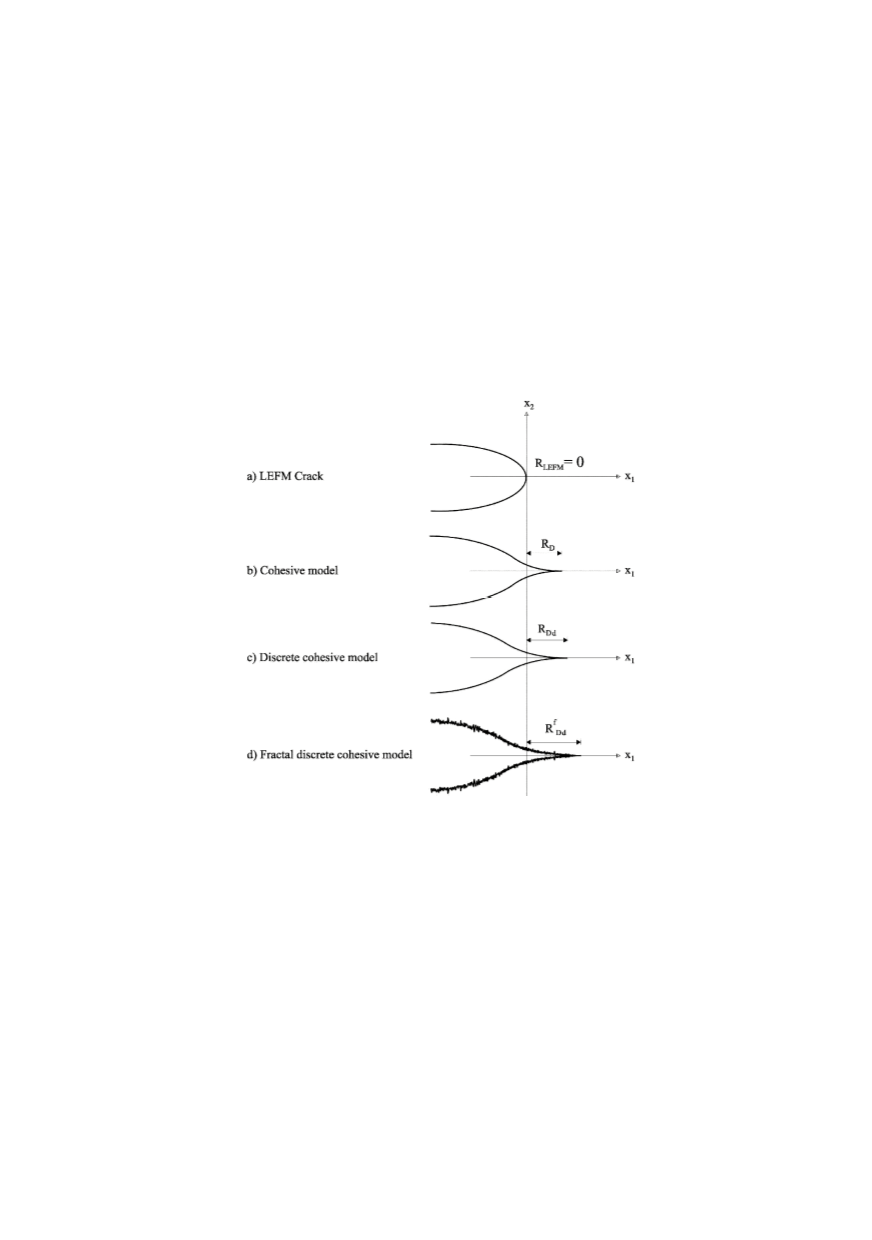
Figure 6 shows schematically four sketches of a crack represented by four different
mathematical models.
Figure 6: Schemes of mathematical models for crack representation
(a) the LEFM concept of a Griffith crack embedded in a linear elastic solid,
(b) Dugdale-Barenblatt cohesive model;
(c) discretetized cohesive model and;
(d) a fractal cohesive and discrete model.
The very first crack shown in Fig. 6 has no cohesive zone at all, and the stresses are
singular at the tip of the crack. In this case fracture toughness must be measured by
employing the ASTM standards that make no mention of cohesion. The second crack in
the figure corresponds to a cohesive model suggested independently by Barenblatt /28/
and Dugdale /29/. With cohesion included a better insight into material response to frac-
ture is involved by visualizing the effect of the cohesive zone. As it turns out, it is a
certain integral of the cohesion stress
S(x)
over the zone
R
. For a constant
S
and under the
restriction of
R
/
X
<< 1 this integral reduces to a product of
S
and the square root of length
R
. This is the Barenblatt cohesion modulus, which determines material resistance to onset
and propagation of fracture. Here, this expression is generalized for a discrete fracture


















