
319
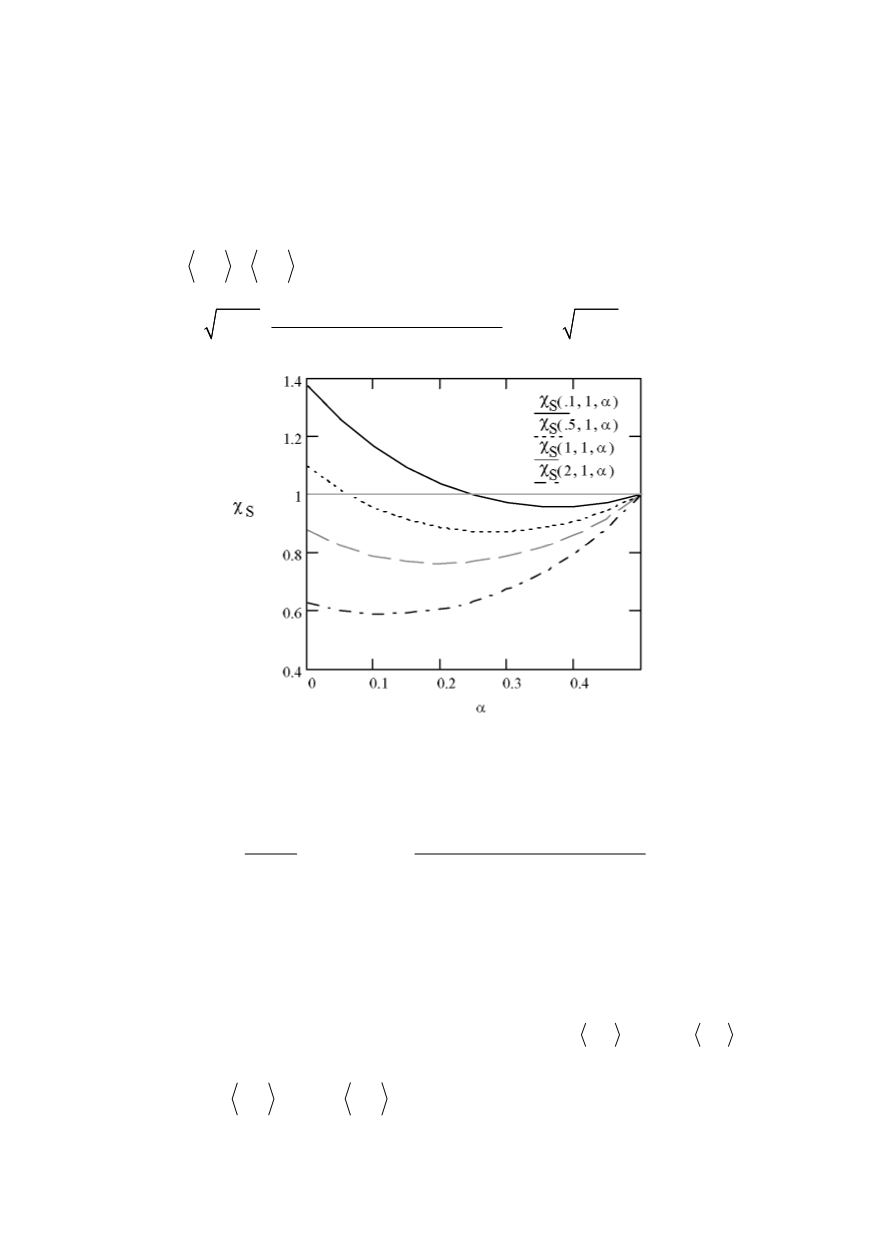
material toughness measured for fractal and discrete fracture, as given by Eqs. (36), (40),
can be either enhanced or reduced when the set of the independent variables (
X
, R,
α
) is
modified. The range of
χ
S
> 1 corresponds to an enhancement of material resistance to
crack initiation due to variations in the degree of fractality of crack surface. The enhance-
ment is seen to occur for the fractal dimension
D
approaching 2 and crack sizes small in
comparison to the constant
a
0
. The effect is pertinent to nano-cracks.
Now all the entities needed to set up the finiteness condition are available. Recalling
the equality
f
f
S
K K
σ
=
and using Eqs. (28), (36) it is arriving
at
1/2
2
2
0
0
2 1
2 1
2 1
( )
( , , )
(
1)
(
)
f
coh
a
S a G X R
X R
X R
α
α
α
α
α
χ α σ π
π
α
+
+
⎡
⎤
+
=
⎢
⎥
+ +
− +
⎣
⎦
(41)
Figure 5: Dependence of function
χ
S
on fractal exponent
α
and two length-like variables
X
and
R
This can be solved implicitly for the loading parameter
Q
f
(
/ 2
f
S
πσ
=
) as a function
of
X
,
R
and
α
. The solution is
1/2
2 1
2 1
2 1
( , , )
2 ( )
(
1)
(
)
f
f
coh
Q
G X R
X R
X R
α
α
π
α
α
χ α
+
+
⎡
⎤
+
=
⎢
⎥
+ +
− +
⎣
⎦
(42)
5. CONCLUSIONS
Relations between applied load and the equilibrium length of the cohesive zone have
been established for three different mathematical representations of the crack, as follows:
1. Cohesive crack model of Dugdale-Barenblatt for a smooth crack described by two
K
-factors
K
σ
and
K
S
corresponding to the applied and the cohesive stress, respectively,
2. Discrete cohesive crack model described by the averages
0
c a
K
σ
+
and
0
S c a
K
+
.
3. Discrete and fractal cohesive crack model involving the fractal equivalents of the
averages, namely
0
f
c a
K
σ
+
and
0
f
S c a
K
+
.


















