
167
In pressure equipment the greatest significance have initial cracks (notches) induced
by machining, heat treatment or welding, and in service the effect of variable stress
amplitudes, affecting both crack initiation and crack extension.
Design of pressure equipment is greatly affected by success in analytical, numerical
and experimental determining of linear-elastic or elastic-plastic fracture mechanics para-
meters. In the case of analytical and numerical determination parameter is crack driving
force due to external load in experimental approach material crack resistance is obtained.
Cylinder or plate with surface crack is most important in practice, because imperfec-
tion in real structures can be presented in this form. There are analytical solutions for
numerous cases depending to loading type (tension, flexion), imperfection position
(surface or internal), imperfect shape (crack, semi-elliptical or semi-circular defect).
Analytical determining of stress intensity factor
In general case of cylinder with defect, solutions for stress intensity factor could be
presented as /5/:
(
)
I
m b
a a a
K
H
F ,
Q t c
π
σ
σ
⎛
⎞
= +
⋅ ⎜
⎟
⎝
⎠
(1)
where
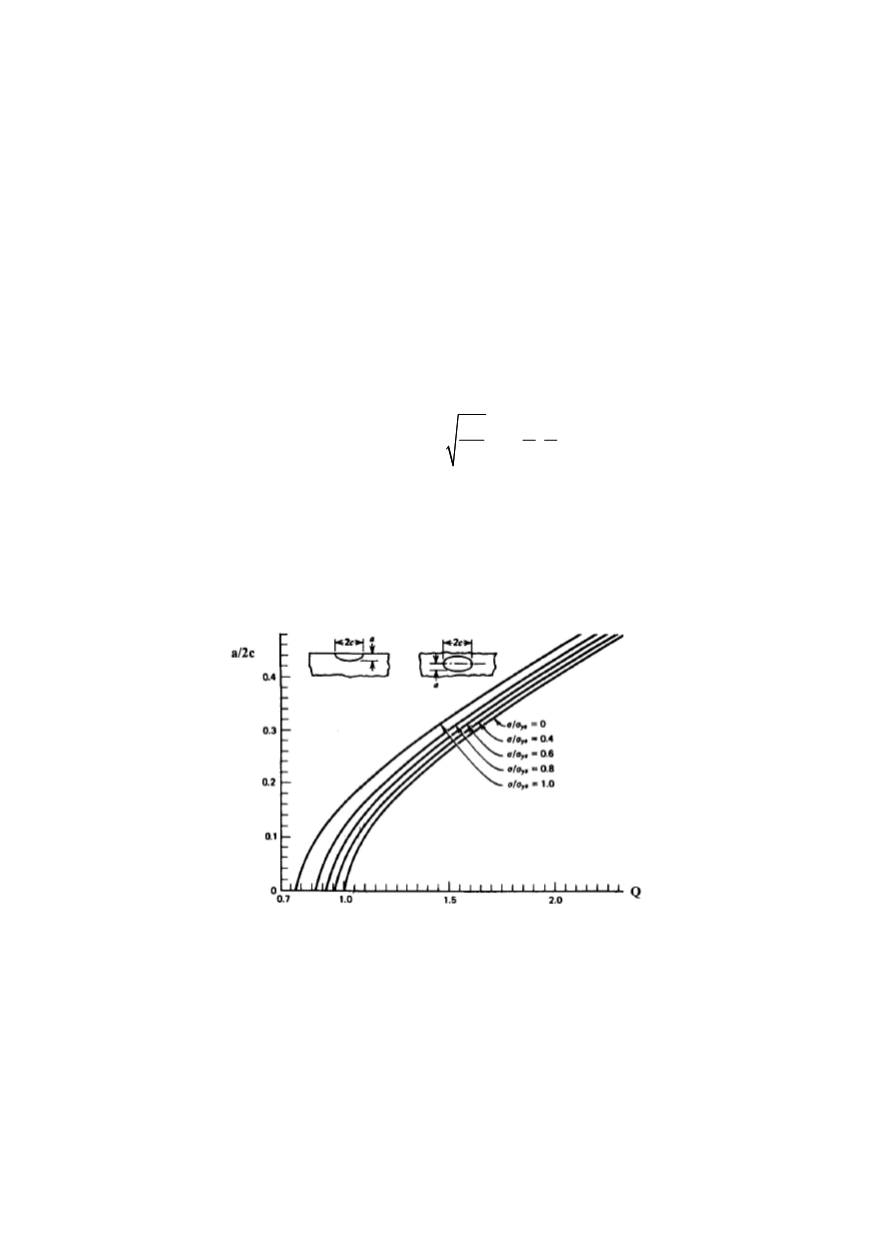
Q
is imperfection shape factor,
a
- depth , 2
c
- length of defect, t - thickness,
σ
m
–
tensile and
σ
b
- flexural component of stress,
F
and
H
are parameters which depend on
ratios
a
/
c
and
a
/
t
. Dependence of factor
Q
on crack shape and applied stress level
σ
/
σ
ys
(
σ
is applied stress,
σ
YS
- yield stress) is shown in Fig. 5. This dependence implies
Q
tends to maximum unique value (
Q
= 2.5) for
a
/2
c
→
0.5, changing the shape from
elliptical to circular, saving in further growth that shape.
Figure 5:
Imperfection factor
Q
dependence of on the crack shape
and applied stress /5/
Analytical determining of CTOD and J integral
There are many analytical models for calculation of crack tip opening displacement,
δ
t
, (CTOD) and
J
integral /6/. They are based on empirical relations, like CTOD design
curve and
JWES
empirical formulae, or on simplified mathematical models, ETM and
EPRI as simple, and Read-King’s and Ratwani-Erdogan-Irwin (REI) models as complex,
but very efficient. They will be shortly presented in next text.
Empirical expressions which connect CTOD (
δ
t
) with a remote stress (as a
loading
measure) in elastic and plastic region are based on CTOD curve7/.


















