IFMASS10

71 / 352

67
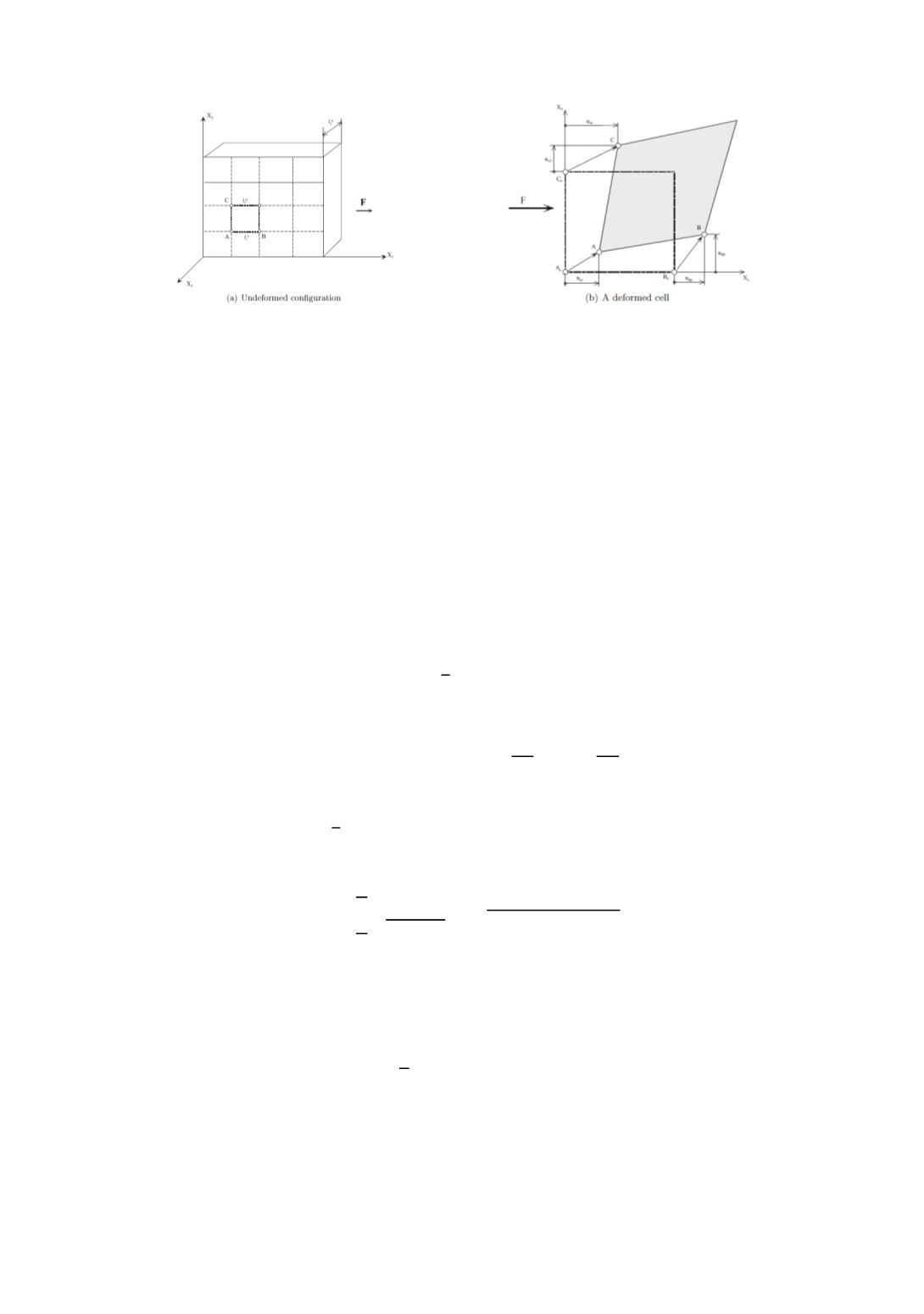
Figure A2: In-plane grid measurements.
Lagrangian total strain tensor:2FൌF்F‐1ൌቐ ܧଵଵ ܧଵଶ ܧଵଷ ܧଶଶ ܧଶଷ ݕݏ݉ ܧଷଷ ቑ (A.3)
Eulerian total strain tensor: 2eൌ1‐Fି் F ିଵ ൌ F ି்EF ିଵ (A.4)
Lagrangian plastic strain tensor:E௉ ൌ ሾ1 െ 2ߙሺΘ െ Θ଴ሻሿE ‐ αሺΘ െ Θ଴ሻ1 ‐ F ି் E௘F (A.5)
Eulerian plastic strain tensor (under the assumption F௘ ൌ R ௘U௘, R௘ ൌ 1): e௉ ൌ ሾΘ െ Θ଴ሿe െ ߙሺΘ െ Θ଴ሻ1 ൅ E ௘e ൅ eE௘ െ E௘ (A.6)
Hill's logarithmic plastic strain tensor:ߝ௉ ൌ ଵ ଶlnሺF௉F௉்ሻ (A.7)
Cauchy (true) stress tensor and its deviator:Tൌ ൝ߪଵ 0 0
0 ߪଶ 0
0 0 0 ൡ , ߪଵ ൌ ܨଵ ܣ ଵ ߪ ,ଶ ൌ ܨଶ ܣଶ ሺA.8ሻ
T'ൌ ଵ ଷ൝ 2ߪଵ െ ߪଶ 0 0
0 2ߪଶ െ ߪଵ 0
0 0 െߪଵ െ ߪଶ ൡ (A.9)
Mises equivalent true stress (compare (A9)):ߪ௘௤ ൌ ඨ 3 2 ඥܚܜሼT'ଶሽ ൌ ටߪଵ ଶ൅ ߪଶଶെ ߪଵߪଶ ( A10 )
Second Piole-Kirchhoff stress tensorS ൎ T െ E௘T െ TE௘ (A11)
Hooke's law: E௘ ൌ ଵ ாሾሺ1 ൅ ߥሻS െ ߥ1ݎݐ Sሿ (A.12) ܧ E௘ ൌ ሺ1 ൅ ߥሻሺT െ E௘ െ TE௘ሻ െ ߥ1ݎݐሺT െ E௘T െ TE௘ሻ (A.13)
should be solved iteratively to find Ee from T: Nominal (engineering) stress tensor: T௘௡௚ ൌ ሺdetFሻTFି் (A.14)
Mises equivalent engineering stress (from (A.14):