IFMASS10

60 / 352

56
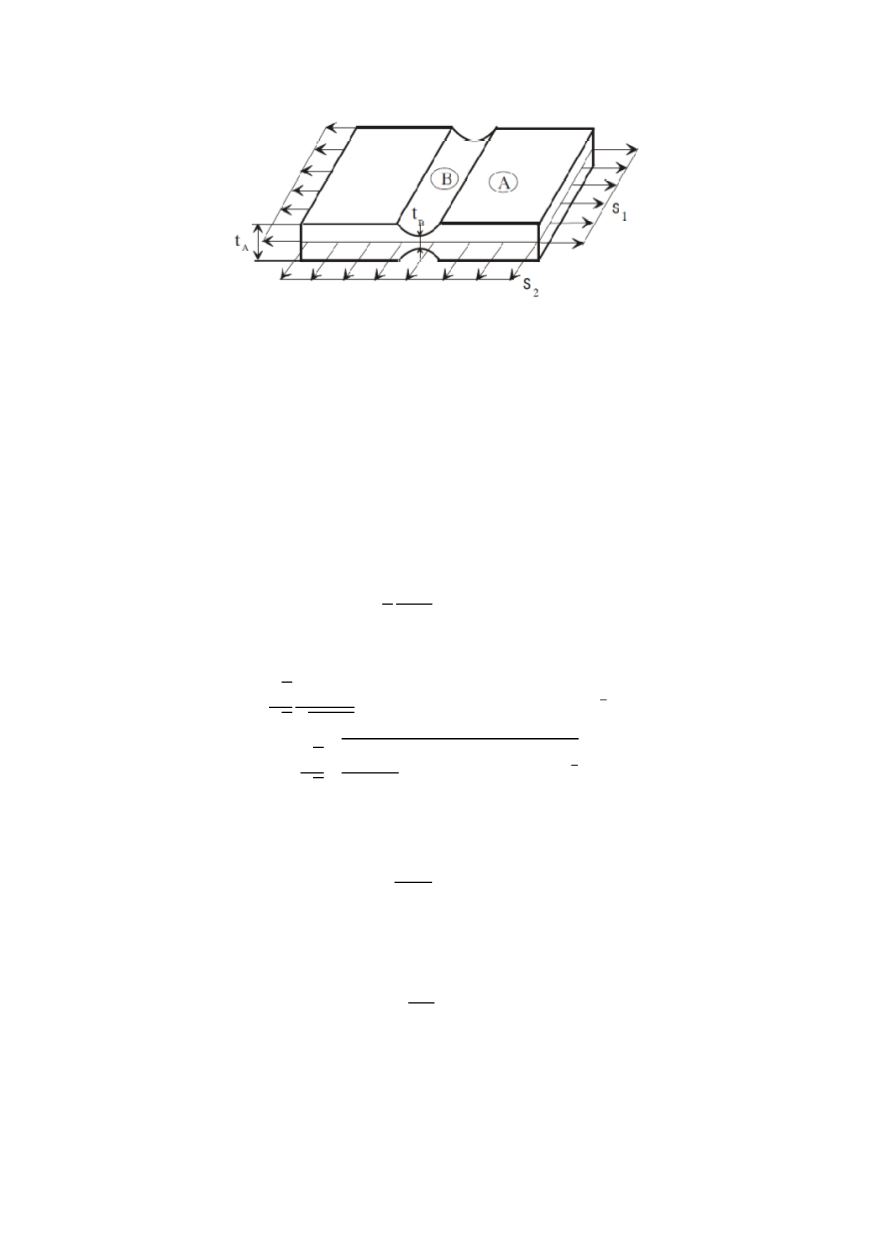
Figure 4: The thin sheet with groove of Marciniak and Kuczynski /22/
Assumptions
A4-1. For the plane sheet specimen considered (Fig. 4) an initial geometric imperfec-
tion given by two symmetric very shallow grooves 1 െ ݐ஻బ ݐ஺బ ا 1 ⁄is assumed. More-
over, a plane tension is considered such that one of principal stresses is along the groove
whereas, the other is perpendicular to it such that stress state is close to equibiaxial
(i.e.ߪ ଵ ൐ ߪଶ ൐ ሺߪଵ 2⁄ ሻ ൐ 0, ߬ଵଶ ൌ ߬ଶଷ ൌ ߬ଷଵ ൌ 0).
A4-2. Rigid rate independent plasticity of transversely isotropic material (its direction
being normal to the sheet) is accepted with evolution equations݀ߝଵ ൌ ሾሺܴ ൅ 1ሻߪଵ െ ܴ ߪଶሿ݀ ,ߣdߝଶ ሾെܴߪଵ ൅ ሺܴ ൅ 1ሻߪଶ ሿ݀ ,ߣ ݀ߝଷ ൌ െሺߪଵ ൅ ߪଶሻ݀ߣ (52)
originating by the associate flow rule from the following yield function2݂ ؝ 2 3 ߪതଶ
݄ሺߝҧሻ ൌ 1 (53)
where ݄ሺߝ ҧሻ is hardening function. Here equivalent stress and equivalent strain increment
are respectively given byߪത ൌ √3 √2 1 √2 ൅ ܴ ሼሺܴ ൅ 1ሻሺߪଵଶ൅ ߪଶଶሻ െ 2ܴ ߪଵߪଶሽభ మ (54)
݀ߝ ҧ ൌ √2 √3 ඨ 2 ൅ ܴ 1 ൅ 2ܴ ሼ݀ߝଵଶ൅ ݀ ߝଶଶ൅ ܴ ݀ߝଷଶሽభ మ (55)
which follow from Korhonen's expressions assuming that R1 = R2 = R. Their product
amounts to the infinitesimal increment of plastic work, i.e.݀ߝ ҧ ؔ ݀መ ܹ௉ ߪത ൎ ݀ߝ ҧ
௉ (56)
The two formulae (54) and (55), are also derived directly from the book of Hill /28/
(chapter on
anisotropic plasticity) with the yielding anisotropy parameterܴ ൌ 2 ߪ௬య ଶ
ߪ௬భ ଶ െ 1 (57)
(ߪ௬భ ൌ ߪ௬మ ് ߪ௬య are uniaxial yield stresses in indicated directions). Apart from a
typographic mistake in ݀ߝ ҧ (where on RHS in M-K they have ߝଵଶ൅ ݀ ߝଶଶ൅ ݀ߝଷଶ), constants
in ߪത and ݀ߝ ҧ are slightly different here, but it does not influence the final results.