
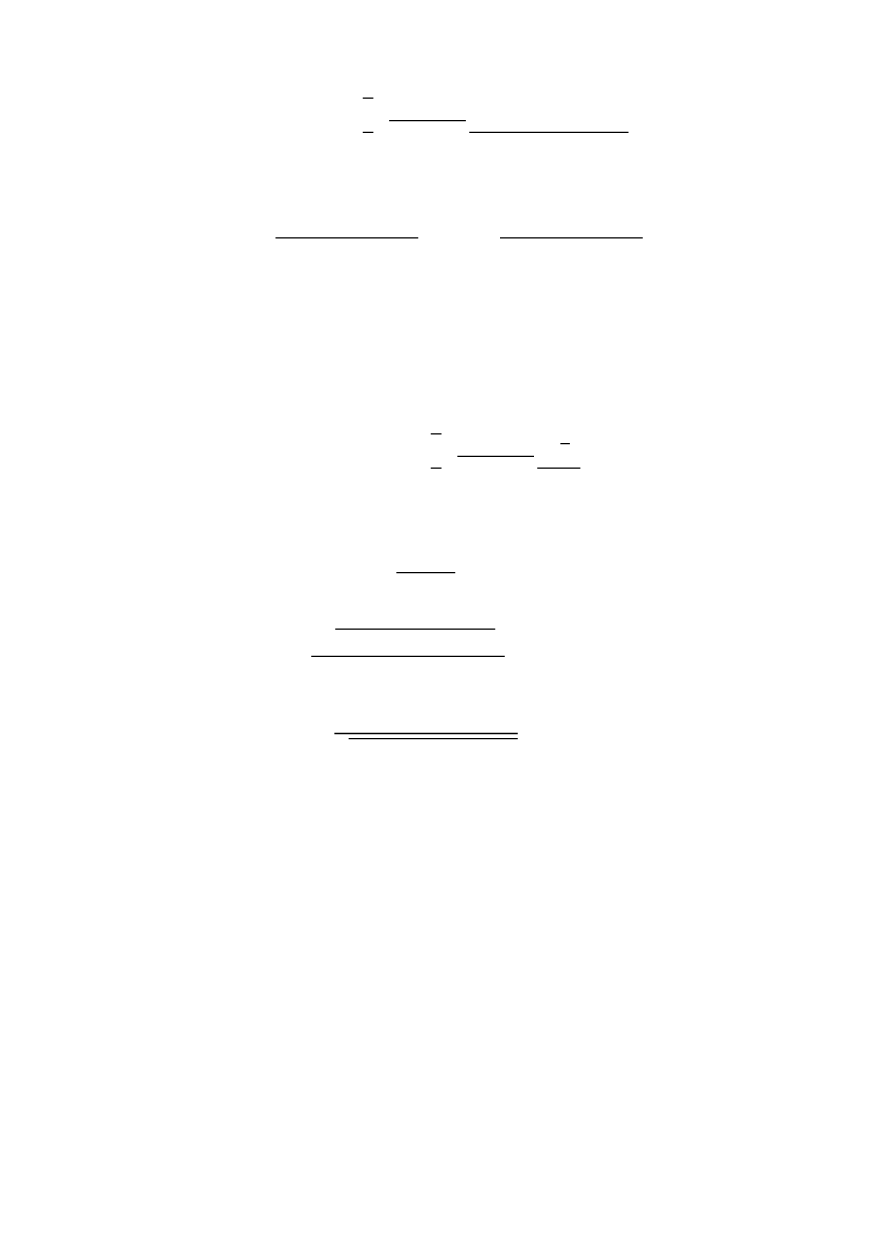
55
ߝ
ҧ
௨
ൌ ܼ݊ ൌ ݊ඨ 2 3 √ܾ ܿ െ 1 ሺܿ െ 2݉ ܾ݉
ଶ
ሻ
ଵ ଶ⁄
ܿ െ 1 ݉ሺܾ െ 1ሻ
(45)
Its in-plane components are found from definition of equivalent strain and Levi-Mises
equations as follows:
ߝ
ଵ௨
ൌ ݊ ܿ െ ݉ ܿ െ 1 ݉ሺܾ െ 1ሻ ,
ߝ
ଶ௨
ൌ ݊ ܾ݉ െ 1
ܿ െ 1 ݉ሺܾ െ 1ሻ
(46)
such that the straight line
ߝ
ଵ௨
ߝ
ଶ௨
݊
(47)
delimits uniform strain state as instability onset. The above equation has been already
written in Ref. /1/ for isotropic solids. Here, it is shown that the same equation holds for
orthotropic solids as well. It is worthy to note that the same result holds irrespective of the
definition of equivalent stress and equivalent strain used. In the special case of uniaxial
stress tension
m
= 0, uniform equivalent strain is reduced to
ሺ
ߝ
ҧ
௨
ሻ
௨
ൌ ܼ݊
௨
ൌ ݊ඨ 2 3 √ܾ ܿ െ 1 √ܿ ܿ െ 1
(48)
Following Ref. /11/ let us define ductility as ratio of general limit strain versus limit
strain at uniaxial tension:
ࣧ ൌ
ߝ
ҧ
௨
ሺ
ߝ
ҧ
௨
ሻ
௨
(49)
This universal measure of instability onset is easily calculated from above formulae:
ࣧ ൌ ඥ1 െ 2݉ ܿ⁄ ݉
ଶ
ܾ ܿ⁄
1 ݉ሾሺܾ െ 1ሻ ሺܿ െ 1ሻ
⁄
ሿ
ؠ
ܶ
כ
(50)
where a modified triaxiality factor
ܶ
כ
ൌ 1 ݉ ሺܾ െ 1ሻ ሺܿ െ 1ሻ
⁄
ඥ1 െ 2݉ܿ ܿ⁄ ݉
ଶ
ܾ ܿ⁄
(51)
reduces to the known form
ܶ
ൌ
ݎݐ
T
ߪ
ത ⁄
in the special case of isotropy when
b
=
c
= 2.
At the end of this subsection the following comments seem necessary:
–
The point that the assumption A3-1 is not connected to the other assumptions and the
analysis subsequently presented above seems interesting. Thus, if the above criterion is
valid, then its validity is not necessarily restricted to strain range
ߝ
ሶ
ଵ
0,
ߝ
ሶ
ଶ
൏ 0
.
–
At first sight the assumption A3-1 seems unquestionable and physically well grounded.
However, if elastic strains are not neglected, then the results hold only for plastic but
not for total strain. On the other hand, plastic volume change could also be significant at
advanced plastic strains due to holes development and coalescence.
2.4. Localized instability due to initial geometric imperfections
Here it is assumed that material instability originates from an initial thinning
developing catastrophically into fracture.
In this field fundamental is the contribution of Marciniak and Kuczinsky /22/. In the
literature dealing with the subject their approach is denoted by M-K for brevity.
Another paper to be considered is /21/. It is also purely analytical aiming to compare
criteria dealt with diffuse and localized instability.


















